Power Supply Design Notes: SPICE Thermal Models

Simulations with thermal models are used to make a rough estimate during the initial phase of thermal design. Devices that implement thermal behavior can be used to process and produce results in the temperature domain.

The SPICE model does not have the commands to directly manage the components and thermal behaviors of a system. However, there are SPICE models that can be used to perform simulations in relation to heat, thanks to the implementation of particular mathematical equations. They are defined as “thermal models.” Simulations with thermal models are used to make a rough estimate during the initial phase of thermal design. Devices that implement thermal behavior can be used to process and produce results in the temperature domain.

SPICE standard and thermal models

Normal SPICE models of electronic components describe the characteristics of typical devices. In most cases, such models can be a useful tool for evaluating component performance. Obviously, they cannot predict operation in all working conditions, and therefore, they cannot accurately model the performance of the device in all conditions, especially thermal ones. Therefore, today, the following simulation models can be found:

Generic SPICE models
SPICE thermal models

The former, in their internal description in SPICE language, are characterized by the presence of only the electrical and electronic terminals that characterize the component. For example, the following is a UF3C065080T3S MOSFET characterized by only the three terminals: drain (nd), gate (ng), and source (ns).

********************** D G S

.subckt UF3C065080T3S nd ng ns

Ld nd nd1 5n

Lmd ns1 nd2 2n

Ljg ng1 ns3 4n

…………

xj1 nd1 ng1 ns1 jfet_G3_650V_Ron params: Ron=75m Rgoff=1.3 Rgon=1.3

xm1 nd2 ng2 ns2 mfet180

.ends

The latter, on the other hand, also has the textual description of the typical thermal parameters, as well as the electrical ones. As you can see, in addition to the usual terminals of the MOSFET (1 = drain, 2 = gate, and 3 = source) they also report other thermal parameters, which are also on the graphic model of the component:

For example the following is a SCT3017AL_T MOSFET characterized by the terminals drain (1), gate (2), source (3), Tj, Tc, Ta.

********************D G S Tj Tc Ta

.SUBCKT SCT3017AL_T 1 2 3 Tj Tc Ta

.PARAM T0=25 T1=-100 T2=600

.FUNC K1(T) {MIN(MAX(T,T1),T2)}

V1 1 11 0

L1 3 32 4.1n

…………

R2 3 32 10

C1 23 12 1p

C21 Tj Ta 1.234m

.ENDS SCT3017AL_T

The models shown have obviously been simplified and are not complete. As can be seen in Figure 1, what distinguishes a traditional SPICE model from the thermal one is precisely the header line, in which the electrical terminals and/or the thermal terminals of the component are listed.

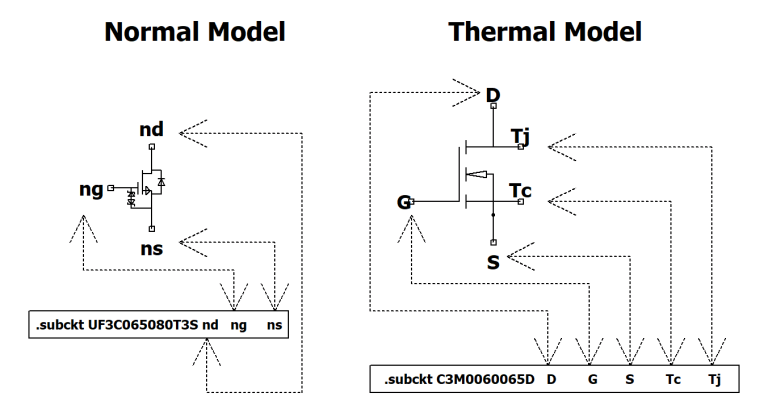
Figure 1: Traditional SPICE model and a thermal model

The thermal model

Usually, the thermal model is slower in the simulation because, in addition to the calculations of the normal electrical and electronic behaviors, the simulator has to process all the thermal equations of the system, and this involves a lot of computational work. The new terminals of a thermal model are as follows:

Tc (case temperature)
Tj (junction temperature)
Ta (ambient temperature)
Tjd (junction temperature for diodes in the MOSFET)

The temperature connections function as the voltage nodes and are electrically separated from the electrical part. A model may have some of these parameters, and not necessarily all of them. Usually, the junction temperature is included in the model, so the user only needs to define a “case temperature” and the ambient temperature. Other times, it is the user who must also define or query the junction temperature. Thermal nodes Tj and Tjd allow the user to easily monitor the simulated junction temperature. Usually, these nodes shouldn’t be connected. The thermal node Tc contains the temperature information on the case of the component.

Note that in a thermal model:

The voltage in a node indicates the temperature, expressed in °C.
The resistance indicates the thermal resistance, expressed in °C/W.

To fully understand how the thermal transition works, imagine the system as a set of resistors that limit the action of temperature, as can be seen in Figure 2.

Figure 2: Temperature passes from one component to another according to its shape, size, and material.

A practical example

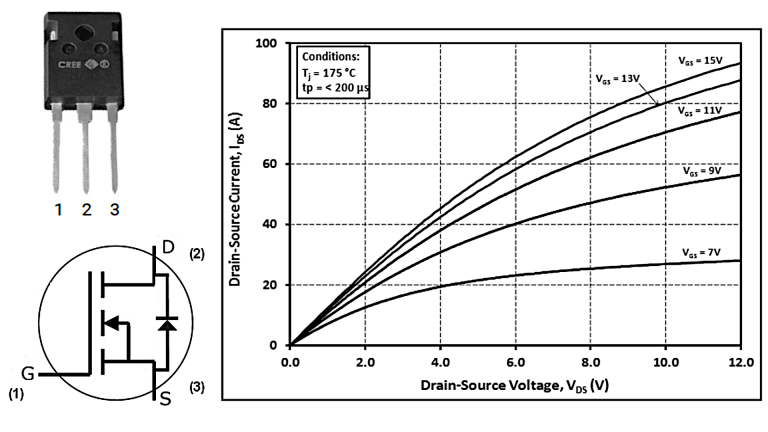
The following practical example uses a Cree C3M0060065D SiC MOSFET model, shown in Figure 3. It is a component in a TO-247-3 package and has the following characteristics:

Vds: 650 V
Id: 37 A
Id (pulsed): 99 A
RDS(on): 60 mΩ
Can be easily connected in parallel with other specimens
Case: TO-247-3
Vgs: Between –8 V and 19 V (the recommended voltage is: 15 V [on], –4 V [off])
Pd: 150 W
Tj: Between –40°C and 175°C
TL: Maximum sealing temperature of 260°C
Rjc: 0.99°C/W
Rja: 40°C/W

Figure 3: Cree’s C3M0060065D power MOSFET

The diagram in Figure 4 shows a classic electronic switch that supplies a resistive load of 10 Ω with a power supply of 96 V (for a current on the load of about 9.6 A). Let’s examine the electrical characteristics of the scheme:

Gate voltage recommended by the MOSFET datasheet (V2): 15 V
SiC MOSFET used: C3M0060065D by Cree
Load resistance: 10 Ω
Circuit power supply voltage: 96 V

Let’s now examine the thermal characteristics of the scheme:

Ambient temperature: 25°C
Thermal resistance of the heatsink (R2): 20°C/W

Therefore, despite the fact that the wiring diagram is using a voltage generator of 25 V and a resistor R2 of 20 Ω, such components are intended to configure only the thermal system and have no functionality on an electrical basis.

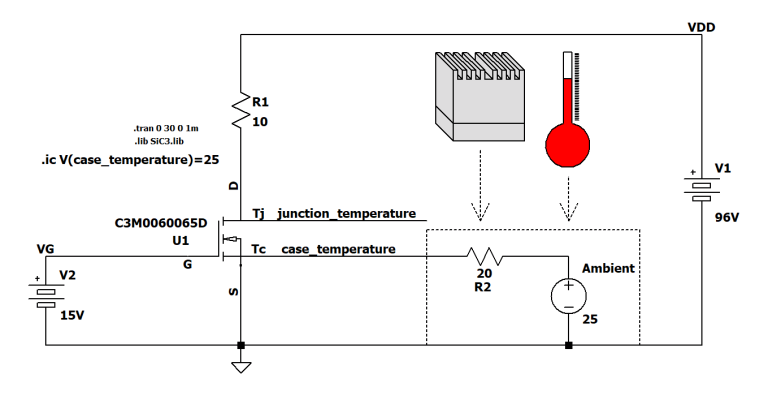
Figure 4: Wiring diagram of the thermal prototype

In the wiring diagram, it is very important to set the initial temperature of a node also using the following SPICE directive:

.ic V(case_temperature)=25

Calculation of the operating temperature

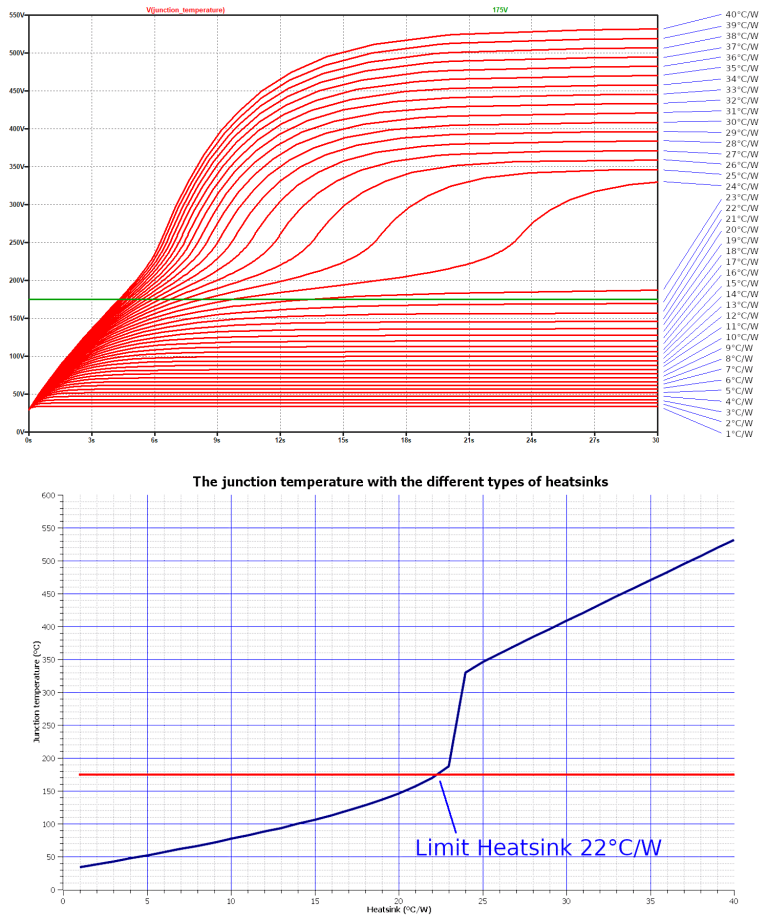
The component datasheet states that the maximum junction temperature is 175°C. Let’s see how the various heatsinks behave with the resistive load considered above, also looking at the graphs of Figure 5. When the temperature system reaches equilibrium, the simulator can measure the following temperatures:

20°C/W heatsink: Junction temperature 146°C, case temperature 140°C. Thermal equilibrium is reached in about 20 seconds.
5°C/W heatsink: Junction temperature 52°C, case temperature 47°C. Thermal equilibrium is reached in about 4 seconds.

In any case, the component works regularly, as its junction temperature is below the maximum limit of 175°C. With the heatsink of 20°C/W, the operation of the MOSFET is almost at the limit. Note that the graph shows voltage as a unit of measurement, but in reality, the temperature is being measured. If no heatsink is used, or if its measurements and performance are reduced (for example, 20°C/W), the MOSFET will be destroyed after 7 seconds and the theoretical thermal equilibrium point is over 500°C.

Figure 5: Measuring the temperature of the junction and the case, with different types of heatsinks

Determination of the ideal heatsink

A stepping simulation allows establishing and determining the best type of heatsink in the system created. The directive to be used is:

.step param heatsink 1 40 1

to examine the behavior of all heatsinks with a thermal resistance between 1°C/W and 40°C/W, as can be seen in the graph in Figure 6. For the circuit designed in this article, a good heatsink must have a resistance thermal range between 1°C/W and 22°C/W. Otherwise, the MOSFET is destroyed.

Figure 6: Simulation of the different types of heatsinks

The ambient temperature on the SiC MOSFET

Designers looking at the datasheets of the MOSFETs feel safe, observing that the junction temperature can easily handle 175°C. This might indeed seem a hardly reachable limit. But the reality is quite different, and in this paragraph, we can observe that the ambient temperature affects the components in a decisive way. Suppose that the previous circuit is characterized by the following electrical and thermal parameters:

Heatsink with a thermal resistance of 20°C/W
Ambient temperature between –40°C and 70°C (a realistic situation)

For this type of analysis, it is necessary to carry out a DC simulation with a precise range, as the ambient temperature is determined by a voltage generator. The SPICE directive to perform the analysis is as follows:

.dc Ambient -40 70 1

In Figure 7, it is possible to observe the graph of the junction temperature (Tj) of the MOSFET (in the y-axis) in reference to the ambient temperature (in the x-axis). As you can see, the circuit can work properly with an ambient temperature of up to 40°C. Above this value, the MOSFET could be seriously damaged unless a more efficient heatsink is adopted.

Figure 7: Ambient temperature has a decisive influence on a system with SiC MOSFETs.

Conclusion

Often, a simple electrical and electronic analysis is not enough, especially with power components. Temperature is an integral part of how high-energy systems work, and forgetting to include it in simulations is a serious mistake.