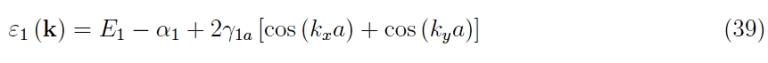Computational Model for Analyzing Wide-Bandgap Semiconductors

Understanding the mechanism of formation of the valence and conduction bands of a semiconductor is of vital importance under the potential technological implications for what concerns the production of new materials.

 

Understanding the mechanism of formation of the valence and conduction bands of a semiconductor is of vital importance under the potential technological implications for what concerns the production of new materials. This work proposes a computational model for wide bandgap that highlights the theoretical difficulties of understanding the band structure and then compares it with the experimental data.

We had concluded the previous work by mentioning the crystalline structure of wide-bandgap silicon carbide. In particular, we looked at the so-called β form with a face-centered cubic as seen in Figure 1.

On the other hand, wide-bandgap gallium nitride has a more complex crystalline structure which is that of wurtzite, a mineral composed of zinc and iron. The basic structure that binds the atoms of zinc and iron is the hexagonal one; the Mathematica software returns the hexagonal lattice as seen in Figure 2. To this, there must be an added structure of the sulphides, as shown in Figure 3.

From the periodicity of the lattice, we expect equally periodic behaviors regarding the material constituents (atoms/ions/electrons) of the solid, which will have to take into account quantum effects. In this modelling, the computational difficulties of wide bandgap are enormous, as can be seen in the graphs shown in Figures 4 and 5.¹ The first chart is evident, while the second illustrates the germanium bandgap as a function of a new quantity k called the wave vector. The latter expresses a periodic behavior of the single electron concerning the crystalline structure due to the wave nature of the electron itself.

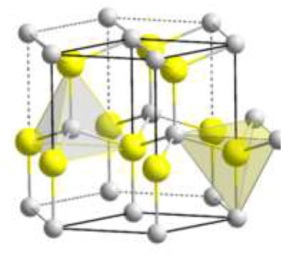
The graph in Figure 5 dates back to the 1960s, following a dense intersection of theoretical and experimental works carried out mainly on silicon and germanium.

In the next section, we propose a simple model that highlights the following peculiarities:

1. The genesis of the allowed bands is favored by values of the lattice parameter comparable with the average dimensions of an atom. This is due to an increase in the density of the atoms making up the solid, which corresponds to an increase in the energies involved that favor the ionization of the atoms themselves, which thus free electrons in any case confined to the lattice (jokingly, they are on the leash of the Bloch waves) making themselves responsible for the transport of electric charge
2. As paradoxical as it may seem, a fully occupied energy band (in the sense that for each energy level we find two electrons with antiparallel spin in accordance with the Pauli exclusion principle) does not conduct an electric current. This is due to the wave nature of the electron: the “game” of the superimpositions/interferences of electronic waves returns (in the full band) standing waves which, as is well known, do not have propagation properties.

Virtual conductor made up of 1023 hydrogen atoms

For now, instead of going into complicated and exotic lattices such as those of wide-bandgap SiC and GaN, let us examine the cubic lattice as the simplest of all, in order to implement a computational experiment whose conclusions, although not universal, provide valuable clues on the phenomenon of transport of electric charge.

The position of atoms/ions/electrons will be referred to as a system of Cartesian Oxyz axes arranged as in Figure 6. Here the primitive vectors have the same length:

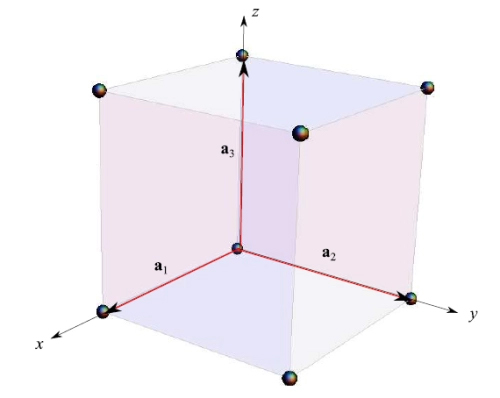
Therefore, we have a single free parameter: the lattice constant a, that is the edge of the cube.
Since we are working virtually, we “add” a hydrogen atom to each vertex, each positioned at

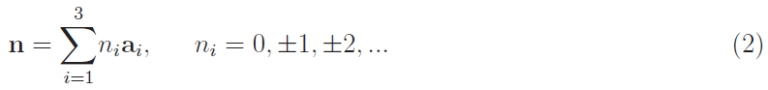
We borrowed hydrogen for two reasons: It is the simplest atom (a proton and an electron), and it is the only one for which the Schrödinger equation, which determines the quantum states of the electron, is solved in closed form.

We consider the single-atom electron in the fundamental level whose energy it is

Quantistically, the electron with such energy is described by a wave function (called the atomic orbital):

where the subscript 1 (both in the orbital and in the energy) reminds us that we are considering the fundamental level. The independent variable is the radial coordinate of the electron:

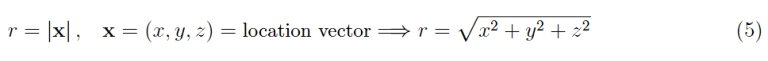
and a₀ ≃ 0.5 Angstrom (1 Angstrom = 10^-8 cm) is the Bohr radius that defines the order of
the magnitude of the linear dimensions of the hydrogen atom. The wave nature of the electron is therefore manifested through an atomic orbital as a wave function, whose interpretation is of a statistical nature: its square modulus is the probability density of finding the electron with an assigned radial coordinate. From the analytical expression of the wave function of the fundamental level, we see that this probability is maximum for r —> 0 and then decays exponentially as r increases.

Therefore, we have infinite atoms each positioned in x – n, where the single electron is in the quantum state:

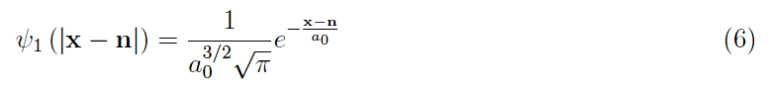
as it is bound to the respective proton by the Coulomb potential:

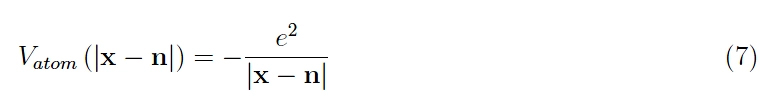
where e is the absolute value of the electron charge. In summary, this virtual solid is assembled by adding hydrogen atoms on each reticular site, starting from an extremely rarefied initial configuration, that is, with a reticular pitch a >> a₀. In this way, the individual orbitals do not overlap by virtue of the exponential decay of their respective amplitudes. However, there is a uniform distribution of atoms and therefore, of Coulomb potentials ⁷. The resulting potential follows:

where the sum is extended to the entire lattice. Therefore, the single electron, while being bound to the respective atom, “feels” the potential V₀ (x). The latter is a periodic function of the Cartesian coordinates x, y, z with the periodicity of the lattice. For Bloch’s theorem, the single electron wave function is a plane wave modulated in amplitude by a periodic function with the periodicity of the lattice. Recall that the spatial part of a plane wave is of the type

where k = (k_x, k_y, k_z) is the propagation vector (or wave vector) whose modulus is related to the wavelength by the relation:

usually called the number of waves, as it returns the number of oscillations in a region of linear dimensions λ. It is preferable to use complex notation, writing the spatial part as

To better define the quantum states defined by the wave vector, we must consider a realistic situation, in which the crystal has a finite extension. This is a big problem as it destroys the periodicity of the potential and therefore, the possibility of applying Bloch’s theorem. Fortunately, the periodicity can be recovered by applying the so-called periodic boundary conditions (or Born-Karman, B-K hereafter). Ideally, considering a one-dimensional crystal on a straight line, we can truncate this sequence to an assigned length L = Na, where a is the lattice pitch (distance between contiguous atoms). The order of magnitude of N is 10²³ which recalls the Avogadro number.

The periodicity of the distribution can be recovered simply by modifying the crystal topology or by bending the truncated distribution axis at L = Na until it closes in a loop. In this way, we find the same distribution even though we go through the loop infinite times. The conditions of B-K are applied to the extremes of the truncated axis and the presence of cos(ka) forces the variable k to assume discrete rather than continuous values. Among other things, this variable defines a “space k” which is a sort of duality of the space defined by the crystal lattice and is called the reciprocal lattice (the attentive reader will understand that the two lattices are connected by a Fourier transform) in which physically significant quantities such as energy exhibit periodic behavior as a function of k, with period 2π/a. Therefore, it is preferable to refer to the fundamental domain

called the first zone of Brillouin or the reduced zone. As stated above, the conditions of B-K determine a sampling of k in a succession of allowed and equally spaced values of 2π. The number of allowed values is equal to N; but N = 10²³ for which we have an extremely dense spectrum of values, i.e. continuous.

What has just been mentioned is immediately generalized to the three-dimensional case. More precisely, the (12) is rewritten for the single component of the wave vector k:

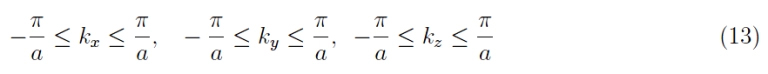
which defines the first Brillouin zone in the three-dimensional case, which obviously exhibits the discrete sampling of the single components. Here we have N³ allowed values for the three-dimensional vector k.

Therefore, we have the appearance of a new quantum number —the wave vector k. For the above, the possible states for a single electron are equal to the number of values allowed for k, i.e. N³ which is then multiplied by a factor of 2, equal to the number of electron spin states for each value of k (the electron spin is quantized and can assume only two values that define antiparallel vectors). Furthermore, the single-electron wave function is an atomic orbital ψ1 and at the same time, it must be an amplitude modulated plane wave, according to Bloch’s theorem. Using a suggestive but effective language, we can assert that the electron rides atomic orbitals through a linear combination such as:

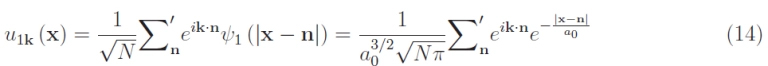
which in turn is a Bloch wave function (as it is modulated in amplitude). The superscript in the summation indicates that the sum is extended to the sample of size (per edge) Na. The factor that appears in front of the summation is normalization (by definition of probability). As long as it is a ≫ a0 the orbitals do not overlap, and the electron, despite having 2N³ states available, keeps its energy E₁ = −13.6 eV. However, in the implementation of the virtual crystal, we must necessarily reduce the lattice parameter until it is comparable with the Bohr radius a₀. This results in an overlap of atomic orbitals, and this effect can be treated perturbatively by means of quantum mechanics. Basically, the single electron begins to predominantly “feel” the Coulomb potential of the contiguous atoms. To be more specific, the time-dependent perturbation theory — well known in quantum mechanics — returns a splitting of the E₁ level in a set of 2N³ values that make up an almost continuous spectrum, each for each value of k. We have what is technically known as an energy band.

The perturbation theory returns, at the minimum non-zero order, the following result as regards the energy of a single electron:

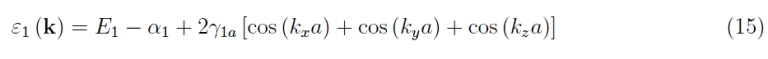
Here we have kept the subscript “1” as the procedure can be repeated for the exciting levels of the hydrogen atom (if we consider states with zero orbital angular momentum, otherwise the situation becomes more complicated). From the calculation it emerges that the term α₁ is positive, therefore appearing with the opposite sign determines a depression of the energy E₁. But the interesting term is γ_1a which depends on the lattice pitch and is the amplitude of a sinusoidal oscillation as a function of the components of the wave vector. In other words, this term reproduces the periodicity of the wide-bandgap lattice and therefore, the splitting of the unperturbed level E₁ into 2N³ continuous levels. Otherwise (γ_1a = 0) the energy of a single electron does not depend on k, and the situation would be undisturbed. More in detail, this magnitude is an integral of the superposition of orbitals and is non-zero as the lattice parameter decreases. The term

has an amplitude of oscillation (around E₁ − α₁) equal to 4 |γ_1a|, therefore multiplying by the number of dimensions ³ we obtain an amplitude 12 γ_1a, which is the amplitude of the energy band. It’s clear that

as we are applying a truncated perturbative development to the first order. The graph of the function is a three-dimensional hypersurface (visible in four-dimensional space), so if we are satisfied with only one dimension we obtain

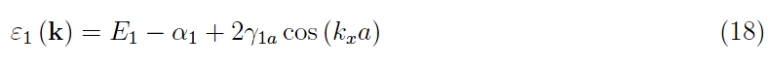
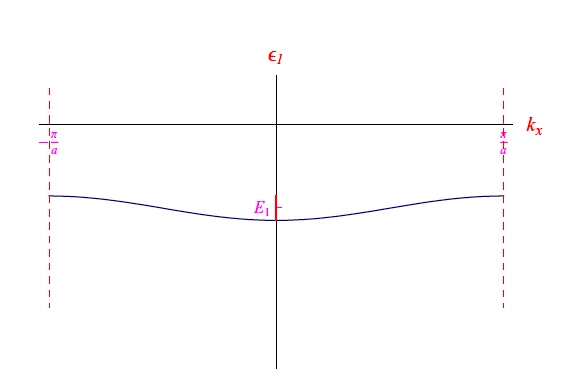
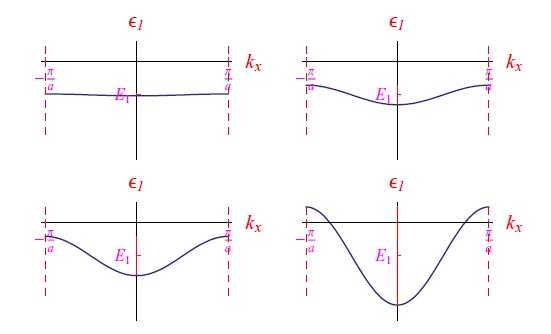
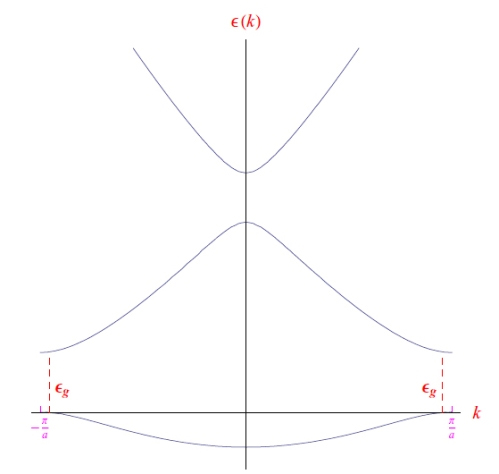
with a typical trend of the type of Figure 7, showing the formation of an energy band.
If we progressively reduce with the software Mathematica the reticular step remaining in the
validity of the aforesaid perturbative development, we obtain the sequence of graphs illustrated in Figure 8. In the last plot appears an interval of energies E > 0, which obviously corresponds to the ionization states of a macroscopic number of electrons. There is no violation of the energy conservation principle since ionization occurs at the expense of the perturbative potential emerging from the presence of contiguous atoms. Note that it is not necessary to apply an electric field to cause a displacement of electric charges, as we have neglected electron-lattice collisions. And it is the latter, as inelastic, that determines the loss of kinetic energy and therefore the impossibility of maintaining an electric current.

We have thus created a virtual conductor in which the electronic conductivity is due to an ionization process that occurs at the expense of Coulomb energy.

Comparison with experimental data

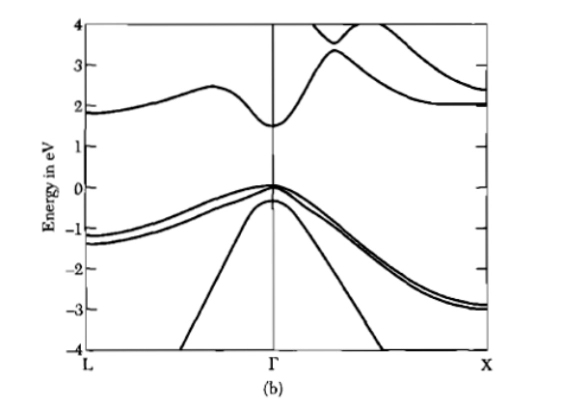
At this point, we compare the graphs of Figure 8 with that of Figure 5 or again with the diagram relating to GaAs as seen in Figure 9, which shows an irregular trend where the symmetry of the function ε (k) is destroyed

Naively this could be due to an anisotropy of the energy distribution law of a single electron as a function of its wave vector. In fact, in the model of the previous section, we considered a simple behavior with respect to the complexity of real conductors/semiconductors.

We then did not consider the electron spin, recalling only that instead of N³ states available, we have 2N³, and in particular, the interaction between the angular momentum of spin and the orbital angular momentum of the electron has been neglected. To know what it is, it is necessary to observe that the various branches that we see in the graphs 5-9 represent the distributions ε (k) for different orbitals, so we rewrite the equation 15 for two successive atomic states n, n 1 (do not confuse the quantum number n with the modulus of the lattice vector). With the meaning of the symbols:

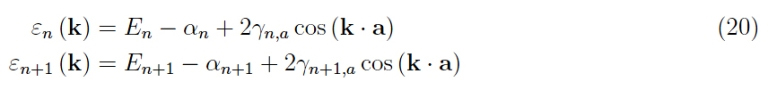
By definition of wide bandgap:

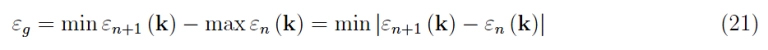
It follows

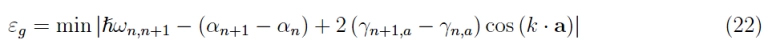
being

That said, the theoretical models that refer to the graphs and to that of silicon that we do not report here, consider atomic states of quantum number n (any excited state), as regards the orbital part they have been with angular momentum l = 1, then taking into account the spin and the composition rules with the orbital moment (i.e. spin orbit), we have j = 3/2 and j = 1/2 which in spectroscopic notation are denoted by p_3/2 and p_1/2. From quantum mechanics, we know that these states are degenerate (the first 4 times, the second 2 times) in the sense that they define physically different states but with the same energy. However, states with higher total angular momentum have higher energy (effect due to spin-orbit interaction). From the same graphs we see that the upper extreme of the valence band is at k = 0 (therefore the parabolic band approximation can be applied as we will see shortly, and which allows us to approximate the ε (k)), while the extremely lower of the conduction band is for k > 0. From the graphs we read the values of the respective wide bandgaps which in any case must be updated as follows:

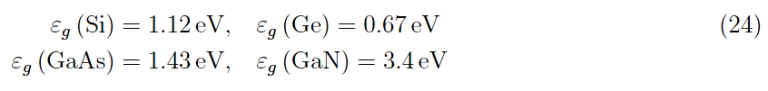
Despite the excessive simplification, the theoretical models’ proposed return interesting results. For example, in the one-dimensional case, a rigorous mathematical analysis shows a band structure of the type shown in Figure 10.

It is therefore fundamental to derive the dispersion law ε (k). This denomination derives from the wave mechanics; so far, we have considered a “snapshot” of the respective Bloch waves describing the propagation of electrons in a solid. We must therefore add the time dependence. The full expression of a monochromatic plane wave is

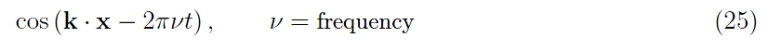
and it is more convenient to write in complex form and in terms of angular frequency:

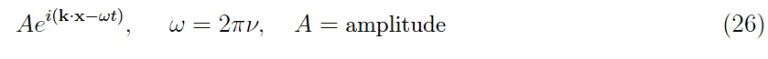
From the Old Quantum Theory (OQT) we know that energy is related to frequency by relationship

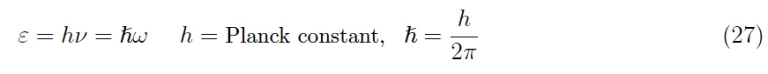
So,

since ε depends on k. Therefore, we have a superposition of monochromatic plane waves to form a wave packet which in the one-dimensional case is written

The velocity of propagation (group velocity) is

which in turn determines, through Newton’s second law which regulates the motion of the electron-wave, an effective mass of this particle, expressed as

whose appearance is due to the presence of the periodic potential of the crystal. In fact, according to the De Broglie hypothesis (OQT) the electron, despite being interpretable through the propagation of a wave packet, has a momentum

which precisely expresses the wave-particle duality. In the law of dispersion found in the previous issue, a cos (ka):

Considering values of k in the immediate vicinity of zero, and developing cos(ka) up to the second order in the Taylor series, we have less than an inessential additive constant:

which is precisely the dependence of energy on the momentum of a particle free from forces, and in this case, the effective mass coincides with the mass of the electron. This simple argument tells us, in fact, that the effective mass of the electron in a crystal expresses the deviation of the dispersion law from (34). Only at the “end of band” i.e. for k — > 0 the electron is approximately free from the periodic potential. In other words, the effective mass is an artifice that allows the electron to be treated according to classical mechanics. In fact, we first applied wave mechanics and then resorted to Newton’s second law. This approach is known as a semiclassical approximation.

Finally, a statistical analysis of the distribution of the energy ε of the electrons shows that if a band is completely occupied, the group velocity of each wave packet is zero — there is no propagation as the superposition of the single monochromatic waves returns a standing wave. This implies that a solid with fully occupied bands is an insulator. However, this conclusion must not be misleading, in the sense that it is valid in the one-dimensional case. The appearance of two other spatial dimensions can determine atypical behaviors as regards the topology of the band structure, in the sense that superimpositions can be created for different directions of the wave vector k, which give rise to conductors rather than insulators. However, it is the electrons of the outermost shells that play the “dirty game.” For example, zinc should be an insulator due to the complete filling of the outermost orbitals. However, due to the particular topology of the respective bands, overlaps have been created that guarantee the possibility of carrying an electric charge.

We conclude this section by observing that the wide-bandgap measurements are performed mainly for:

• The Hall effect
• Cyclotron resonance
• Spectroscopy (in particular for wide-bandgap GaN).

Wide-bandgap SiC

Wide-bandgap SiC has the reticular structure of cubic zinc sulfide (cubic zinc sulfide) which in turn comes from that of diamond (face-centered cubic, FCC). The Zn atoms are arranged on one FCC lattice and the S atoms on the other FCC lattice (Figure 11. Source: [1]).

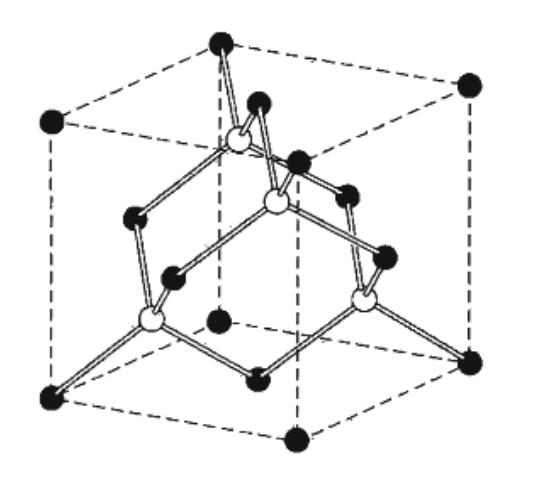
There are four ZnS molecules in each unit cell; around each atom, there are four atoms of different species, equally spaced and arranged on the vertices of a regular tetrahedron.

It is instructive to observe that in all semiconductors (Si/Ge/SiC/GaN etc.), the outermost shells of a single atom of the lattice are of the type (spectroscopic notation):

where n is the principal quantum number, while s and p denote single electron orbital angular momentum states equal to l = 0 and l = 1 respectively. Therefore, we have four valence electrons that form the covalent bond already examined in the previous article. This bond is broken at the expense of thermal energy, and the electrons go into the conduction band. However, this is not a quantum transition, but a statistical mechanism due to temperature.

Wide-bandgap GaN

The case of wide-bandgap GaN is diversified by its technological effects in optoelectronics/photovoltaics, thanks to the possibility of being able to modulate the bandgap by creating new heterostructures such as InGaN, which is a mix of GaN and indium nitride. For now, we limit ourselves to observing that wide-bandgap GaN semiconductors are marking a turning point in the so-called water splitting techniques, i.e., the extraction of hydrogen from water, which could be used as fuel.[4].

Bandgap and temperature

We have already had the opportunity to study thermal stability, in the sense that the bandgap does not significantly depend on the thermodynamic equilibrium temperature T of a semiconductor (Si/Ge/SiC/GaN), less than a factor of the order of 10−4 eV / K. In fact, it is known that [2]-[3]:

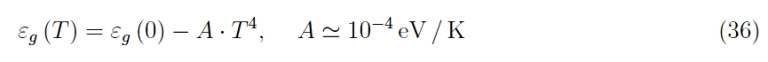
This empirical relation holds in a range [0, T ] with T ≪ Tmax, being

which is the temperature for which the semiconductor behaves like a conductor. Theoretical value, since such a high temperature would lead to the destruction of the device. Furthermore, once an assigned threshold temperature has been exceeded, our model is no longer valid since, as anticipated in a previous section, we are neglecting the motion of the atoms. To be more precise, the model is based on the Born-Oppenheimer approximation, which decouples the motion of electrons from that of atoms since the electrons, being much lighter, exhibit an almost instantaneous dynamic evolution in the time scale of the motion of atoms, which perform “small” oscillations around their respective equilibrium positions due to thermal energy. Asthe temperature increases, the amplitude of the oscillations increases, so we cannot consider the atoms to be “stationary.”

Bloch waves in the one-dimensional case — wide bandgap

In Figure 12 we report the trend of a Bloch wave in the one-dimensional case. Specifically, a lattice is given a linear chain of ions in which the potential is represented by the periodic function:

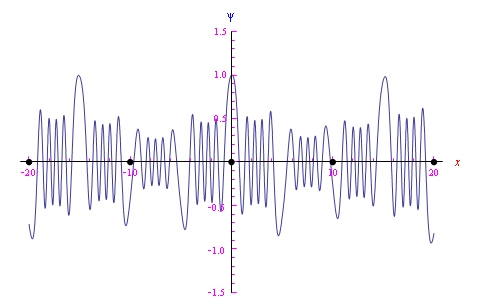
In this case, the Schrödinger equation solves in closed form, and its solutions are the Mathieu functions.

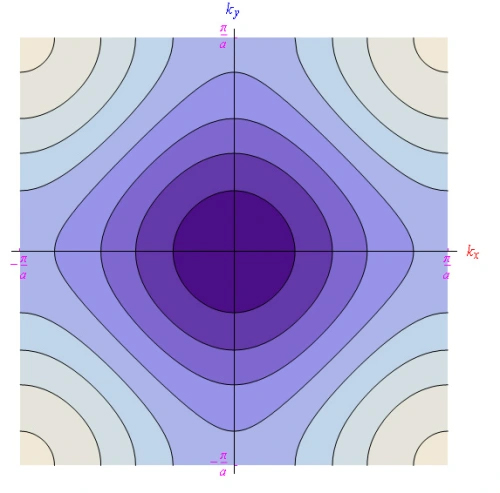
Level curves of the dispersion law

We report in Figures 13 and 14 the shape of the level curves of the dispersion function rewritten in case 2- dim: